归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法的一个非常典型的应用。
分治法将问题分(divide)成一些小问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案“修补”在一起,即分而治之。
算法步骤
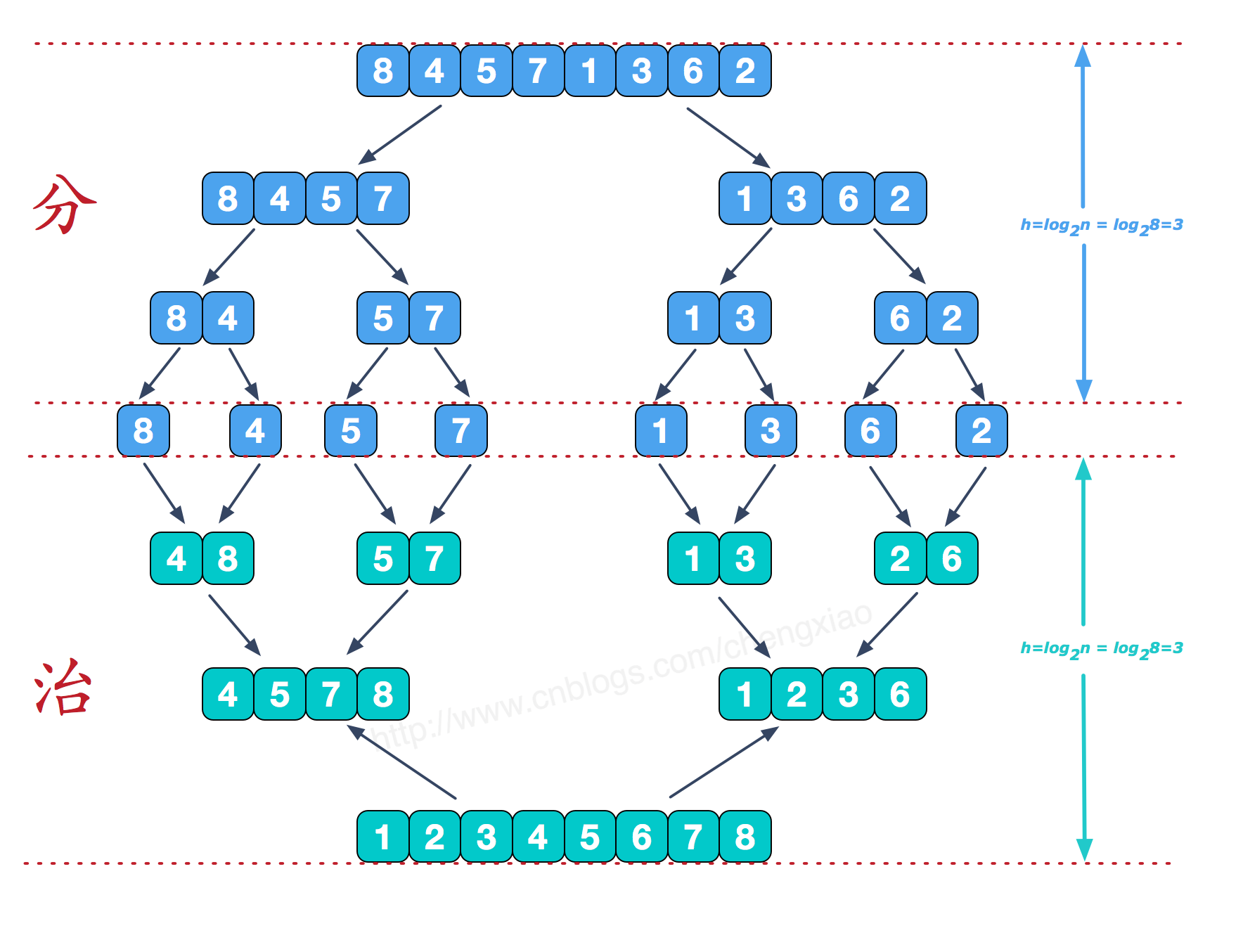
- 自上而下递归拆分子序列,直指子序列只有一个元素;
- 自下而上合并子序列为一个有序序列;
动图演示
代码实现
1 | template <typename T> |
树叶的一生,难道只是为了归根吗
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法的一个非常典型的应用。
分治法将问题分(divide)成一些小问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案“修补”在一起,即分而治之。

1 | template <typename T> |